�@�{���͑�56���Ƃ��ď������Ƃ��Ă����B�����ցu�q�b�O�X���q������!�v�̃j���[�X�����\���ꂽ���߁A56���͋}篗Վ��j���[�X�Ƃ��ăR�����g���邱�Ƃɂ����B����ŁA���̍�����57���ɂȂ����B
�@�{�������ǂ݂ɂȂ�O�ɁA�܂���55�������ǂ݂łȂ����́A���А�ɂ�������ǂ݊肢�����B�Ƃ��Ɂu�����w�̎��R�_�v�̂Ƃ�����B
�@���āA���Θ_�͕s�����ł���A�Ƃ킽���͎咣���Ă����B���Θ_�ɂ��A�d�͏�̈Ⴂ�ɂ���Ď��Ԃ̐i����Ⴄ�Ƃ����B�܂��A�ꏊ�ɂ���Ď��Ԃ͈Ⴄ�Ƃ����B�ƂĂ��^�Ɏ�킯�ɂ䂩�Ȃ��B
�@�������Ȃ���A�킽���ɂ��A�������Ƃ����_�ŁA�܂��悭������Ȃ��A��̕���������B���̓�͉�����̂������Ȃ��̂��A�����������Ȃ�����ǁA������̎��|����Ƃ��āA�u��p����p�̖@���͓�����?�v�Ƃ����Ƃ��납��A�l���Ă݂����B
�͊w�I������ �\�\12.6.29
��p����p�̖@���͓������H
�@�͊w�I��p�ɂ́A���̓`�B�Ɍ��܂�������������̂ł��낤���H
�̖_�Ń_���}������
�@
�@�_���}��}�̂悤�ɁA�̖_�ʼn����Ă݂�B�_���}A�Ɩ_�Ƃ͂��Ă���B
 �@�}1
�@�}1
�_�̂a�[�����̗͂ʼn����A���[�ł͓����Ƀ_���}�`�����̗͂ʼn������낤�B�w�Z�Ŋw�Ƃ���ɂ��A���̂Ƃ��_���}�́A�͂��������������A�����ɂ��̗͂ʼn����Ԃ��Ă���B���̂Ƃ��́g�����h�͐��������낤���H�@��������j���[�g���̉^���̑�3�@���ł����p����p�̖@���ɓK�����Ă���B���������낤���H
�@�Ƃ����̂́A�_�̒������P�q����ł����Ă��A�a�ʼn������͂͂`�ɓ����ɍ�p����ł��낤���H
����ɂႭ�Ń_���}������
�@
�@�ł́A�_���łȂ��A����ɂႭ��������ǂ����낤���H
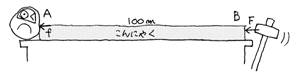 �@�}2
�@�}2
�@�ւ�Ȃ��Ƃ������悤�����A����ɂႭ�͒@�����O���瑶�݂��Ă���B�ڂ̑O�ɂ���ɂႭ�͑��݂��Ă�B�e���Ȃ�F��A���Ȃ��̌��_�͂ǂ����H�@�����Ȃ闝�R�́H
���āA��p����p�̖@���́A�����ɂ̓_���}�`�Ƃ`�ɓ˂������Ă���_���`��˂��͂��Ƃ̂������ŁA�a�[�Ƃa�[��@���Ɓi��p�͂͂e�j�Ƃ̂������ŁA�����Ă���B���ꂼ�ꓯ�m���g�����h�ł���B����Ɩ_�̒��͂ǂ��Ȃ�H�@
����ǂ͓`�B�}�̂��A����ɂႭ��_�Ƃ������g���́h�ł͂Ȃ��ꍇ���l���悤�B�F����Ԃɕ����n���Ɛ��Ƃ̊W���B���Ԃɂ͂ǂ�ȕ��������݂��Ȃ��A�^��ȋ�Ԃ��B
�_������ɂႭ��C���Ƃ����������̉�݂���Q���̊Ԃ̂悤�ɁA�Е���@���Α����ɓ`���A�Ƃ������Ƃ͂Ȃ��B����Ȃ̂ɁA�Ȃ����͓͂����̂ł��낤���B
�n����͂������A���ʂ������Ă��āA���̎��ʓ��m�͂Ђ��������B���̃��J�j�Y���͂������B�n���̎��ʂl�ɂ͏d�͏ꂪ�t�����Ă��āA���̓����ʂ͋�����Ȃ��A�ǂ̔��a�̉��z���ʏ�ł��A���̒P�ʋ��ʐς�����̏�̋��������̋��ʐϑS��4��r2�ō��v�������̂́A�F�������B�����͂�������z�̏d�͐��ŕ\���A���̖{���͕s�ςƍl���Ă���B�܂�A�����قǒP�ʋ��ʐς�����̖{���i��̋����j��1�^�i4��r2�j�Ə������Ȃ�B���ꂪ���̋���r�ł̏�̋������B
���̏�̒��ɒu����鑼�̕��̂̎���m�����̏ꂩ�炤�����p�̑傫���i�d�́j�́A��̋����ɔ�Ⴗ�邪�A���̕��̂̎��ʂɂ���Ⴗ��B���ꂪ���L���̖͂@�����B����͋t�̗���ł������ŁA���̕��̂̂���d�͏ꂪ�n������M�ɍ�p����͂ɓ������B���ʓI�ɁA��p����p�̖@�������藧���Ă���B
����m���������F��
F=�iGM�^r2�j�~m�@
�n��M�����̂��炤�����F��
F=�iG m�^r2�j�~M
�iG�͖��L���͏퐔�B1/4������Ɋ܂܂�Ă���j
�݂��ɓ������B
�@�ł͏d�͏�̑��݂͗L���ȑ����ōL����̂ł��낤���B
�@�L���������Ƃ���A�����Ɠ����ł��낤���H
�@����Ƃ��A���ʂƏd�͂͋��ɂ���A���ʂƂ��̏d�͂̑��݂Ƃ͓����ł��낤���H
�\�\�H��d�͂��@�����H�\�\
�@�L�����x�Ƃ���Ή����N���邩
�@�V�̂`���炠���Ԃɋy��ł���d�͏�́A�V�̂`�̎��ʕω���ړ��ɂ��ω��ɂ�āA�����ɂ��̋�Ԃɋy�Ԃ̂ł͂Ȃ��A���鑬���A�Ⴆ�Ό����œ`�����̂��Ƃ�����A���������ɒn�����P���N�����āi�P�N��Ɂj�Q�ɕ����ꂽ�Ƃ���A�n������P���N�ȉ��ł̒n���d�͏�́A�Ⴆ�P�����N���ꂽ���ɂ́A1�N�O�܂ł̒n���Ƃ��đ��݂��邱�ƂɂȂ�̂ł��낤���H
�@�܂�A�n�������Ă���9999�N�܂ł́A���̐��ɂƂ��ĕ����ɒn����1�Â��ɑ��݂��Ă�����̂Ƃ��Ă̏d�͏�̒��ɂ���̂ł��낤���H
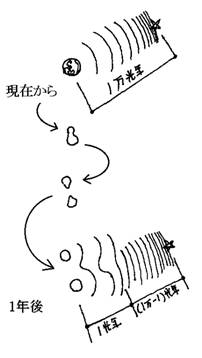 �@�}�R
�@�}�R
�@�܂������A�n���͕��Ȃ�����ɁA�����瓙������ۂ��Ȃ�������ւ`����@�a�ւƂP���N�̋��������Ă����Ƃ�����H�@�P�N�O�ɒn���`��������ꂽ�d�͏�͐��b�̋�Ԃ֒B���Ă��邾�낤�B
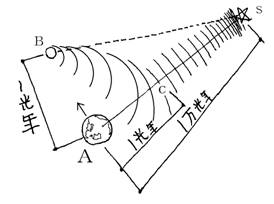 �@�}�S
�@�}�S
�@
�@�}�S�́A�n�����P�N�O�b��Ԃ܂łP���N�������`���瓮���āA���݂a�_�ɂ��邱�Ƃ������B�n���͂P�N�O�ɂ`����ˑR�ɓ����x�œ����o�����Ƃ���A�n�����a�_�ɓ��B�������݂̏u�Ԃɔ�����d�͏�̋��́A�܂��A���قǏ������B����͐��b�ɂ͍������2�N�o���Ă���B���A���̂Ƃ����߂Ăf�a�Ƃ��������x���A���ɗ^���邾�낤�i�}�S�j�B
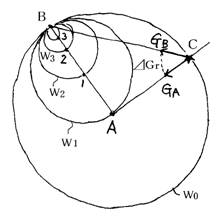 �@�}�T
�@�}�T
�@
�@�}�T�͒n�����a�ւ������_�ɑ��݂���n���̏d�͏��`���Ă���B
�v0�͂P�N�O�ɂ`���甭������A�v1�͒n�����s����1/2�ł���P�܂ł����Ƃ��ɔ��������݂̏�A�v2�͂Q�܂�1/4�������Ƃ��̂��́A�c�Ƃ�������B�����͂��܂a�ɂ���B
�@���������݂͂a����r�����ďd�͏ꂪ�o����������ŁA���܂P�N�O�ɂ`�_����o���d�͏�v0���b�ɒB���Ă���B���̉����x�͂f�`�ł���B�a���݂̂b�����Ɍ����̂łȂ��A�f�`�����ցA�킪�d�͏�͂����ی����Ă���B
�@�n�������b�ɍ�p����d�͏�́A�P�N�O�̂f�`����A�fB�����̏d�͏ꂽ��܂ŁA���̌��������ꂩ��ω����Ă䂭���낤�B
�@�n�������܂a�_�ɂ���Ƃ���ƁA���ł͒n�������݂�������ł͂Ȃ��A�P�N�O�ɒn�������������i�f�`�̌����j�ɓ����Ă��邱�ƂɂȂ�B���ꂪ�������Ƃ���A�^���̑�R�@���u���̂ɗ͂���p����ƁA�����ɐ^���̌����֓������l�ŕ��̂��甽��p����v�ɔw�����ƂɂȂ�B
�@��̗L�������Ɠ������A�ǂ���ɌR�z?
�@�d�͏ꂪ���ʂ̑��݂Ɠ����ł͂Ȃ��A�����ōL������̂ł���Ƃ���A��p����p�̖@���́g�������h�����藧���Ȃ��B���A�n������P�����N���ꂽ���ɂ́A�n�������ɍ�����P�N��ɂȂ��Ȃ��Ă��A����ȍ~��9999�N�Ԃ̂������A���Ȃ�S��̏d�͏�������邱�ƂɂȂ�B�}�S������ł���B
�@�n�����`����a�ւP�N�Ԃ̂������Ɉړ����Ă��A���ւ̏d�͏�́A���ꂩ��9999�N�ԁA�����`���甭����d�͏�Ƃ��ē���������A�Ƃ����킯���B
�@�ړ������P�N��̒n�����猩��ƁA�����͂P���N���������ꏊ�ɋ���ɂ�������炸�A���ł͒n������̏d�͏�x�N�g�������fr�����ω�����͂��̗l�q���������A���ς�炸�����ی������܂܂ł���B�n���̈ړ���10����1���N�ł����Ă����l�ŁA���}�̂悤�ł��낤�B
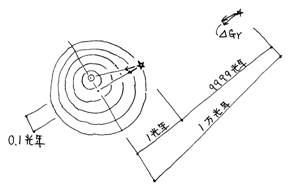 �@�}�U
�@�}�U
�@�t�ɉF����Ԃňړ����Ă���n���ɂƂ��āA������n���ɋy��ł��鐯�̏d�͏�́A�n�����g�̕ω��ɔ����đ����A���̏d�͏ꂩ��̍�p��������B
�@�܂�A��p����p�̖@�����i���������j�����������藧���Ă���B���������ɂႭ�_�����́A�������̒[���i�`�j�����Ă��邩��ł���B���ۂɂ͂��̏ꍇ���A���Ƃ̓������͕ۂ���Ă����A������Ɗ����Ă���d�͏�́A�����P���N�O�ɋ����n�_����y��ł���d�͏�̍�p�������Ă��邱�ƂɂȂ�B
�@�܂萯����n����������d�͏�̉e���́A���̕ω��Ɠ����ɂ͕ω������A�����œ��B����ɕK�v�Ȏ��Ԃ����x��ē����A�n���̕ω������l�ɁA���ւ͓����ɂ͓`���Ȃ��B�n�����g�̕ω��ɂ���Ēn���������炤����d�͏�i�������A����͂P���N�O�ɐ������������́j�́A���g�̕ω��ɉ����đ����ω�����B���Ȃ킿�A���ɒn���̎��ʂ��Q���̂P�ɂȂ�A�����炤����͂͑����ɂQ���̂P�ɂȂ�B�ȏ�́A�����d�͏ꂪ�L���̑����œ`�����̂Ȃ��A�����������ƂɂȂ낤�B
�@
���ʂƏd�͏�͓��ꕨ���\�\012.7.3
�@
�@�����ŁA�d�͏�͎��ʂƓ����ɂ���̂��A����Ƃ�����L���ȑ����A�Ⴆ�Ό����œ`���̂ł��낤���H�@�ǂ��炪���������ɂ���āA�����w�̓��͑傫���������B
�@�킽���͍��̂Ƃ���ǂ��炪���������A�؋����ĂĒf�肷�邱�Ƃ��ł��Ȃ��B�����A�킽���l�̍l���ł́A�d�͏�͎��ʂɕt�����A���ʂƓ����ɂ���B���܂��܂Ȏ��ۂ��ώ@����Ƃ��A�����̏��Ȃ������Ƃ��ẮA���ʂƂ͏d�͏ꂻ�̂��̂ł���A�����͏d�͏�̒��S�����ʂƂ��Ċϑ����Ă���B
�@�܂�A�d�͏�̒��S�����ʂƂ��Ċ�������Ă���B�Ȃ��d�͏ꂪ�W�����鐫���������Ă���̂��B�d�͏���Y��ł�����͉̂������������邱�Ƃ��A�����̒a���̔閧���������������Ă���̂ł��낤�B
�@�킽���̗����ł́A�g�d�͏�͂���L���ȑ����ōL��������h�����ł͂Ȃ��B�C�������łɂ����āA�C�g�͂��̊C���ʂ��C�ʗ͊w�I�Ɂi�����q���m�̑��ݍ�p�Ƃ��āj�g�y���Ă䂭���̂ł���B����䂦�A�g�̐i�s���x�i���ݍ�p�j�͗L���ȑ����������A�C���͂��łɑ��݂��Ă��āA�}���Ƃ��Ă̖����ʂ������̂ł���B
�@���Ɋւ��Ă͏d�͏ꂪ�C���ɑ������A�������C�g�̑����ɑ��������i�d�͏�͎��͓d���g��`�����Ƃ��ĔF�������Ȃ����̂��������̂�������Ȃ��j�B�C�g�͐��[���傫���قǑ����A���͏d�͏ꂪ�����قǑ����B�����͒n�\�ł̏d�͏�ɂ����Ă��i30���q�^�b�j�ł���A�d�͏�[���ł����炭�قڂ��ł��낤�B�d�͏�̑傫���Ƃ���ŁA�����x�������ƂȂ낤�B
�@��͌����i�L�����x�j�Ŕg�y����Ɖ��肷��Ƃ��A�ȏ�̂悤�ɓ����������藧���Ȃ����ƂɂȂ��B���̏ꍇ�A���Θ_�ɂ����A�ꏊ�ɂ���Ď��Ԃ̐i�ݕ����Ⴄ�Ƃ��鉼�����痈��A�����炩�̌��ې����ŁA���R���ʓI�ɍ��v���邱�Ƃ����邩������Ȃ��B�������A���l�������Ƃ͎��Ԃ��Ⴄ�Ƃ��邱�ƂƂ͍��{�I�ɈႤ�B��̓`�B���x���L���ł���A���̒l�������ł���Ƃ����ꍇ�ł����āA�x�N�g���̌����͞B���ȑ��Θ_�ƈ���Ė��m�ł���B
�@�������A�d�͂������ɑ傫���Ȃ�Ό����͖����Ƀ[���ɋ߂Â��킯�ł͂Ȃ��A�d�͏ꂪ�[���Ō����������ɑ����Ȃ�ł��Ȃ��A�Ƃ킽���͍l���Ă���B�܂�A�����͏d�͏�ɑ��Ĉ�ʂɂ��Ƃ݂���L���ȋ����͈͂ɂƂǂ܂���̂ł��낤�ƍl���Ă���B���Z�͂������H
�@�`���ŁA�{�������ǂ݂ɂȂ�O�ɁA�܂���55�������ǂ݂łȂ����́A���А�ɂ�������ǂ݊肢�����A�Ƃ��肢�����B���̂킯�𖾂����Ă��������B
�u�����w�����R�_�v�ɂ���
�@���̍��̌���ŏq�ׂ��A�w�����w�����R�_�x�́A�e���Ȃ�F��A���������ǂ݂��������낤���H�@���Ԃ�A�^���Ȃ��Ƃ��q�ׂ�ꂽ�A���ɂȂ������ł���A�Ƃ������ɂȂ����̂ł́c�B
�@���́A�i.�r.�~���ɂ��w���R�_�x�i���K�����ق����@��g���Ɂj���璼�ڈ��p�������̂��B���́A�P��36�y�[�W����A�Q��39�y�[�W����A�R��41�y�[�W����]�ʂ����B
�@�P�ł́A�u���{�v���u�w�{�v�Ɠǂݑւ��������ŁA�Q���R�ɂ������Ă͈�ӏ������������ւ����Ƃ���͂Ȃ��B�i.�r.�~���Ƃ��̉��l���A�O�O�ɋc�_���d�˂ď����グ��ꂽ�����̂܂܂ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2011�N�@7���@18������
�@